Cube AI

Cube AI is an experimental AI project. The objective was to create a neural network that can solve a Rubiks Cube.
To achieve this goal the I had to overcome the following challenges:
- Modelling a cube
- Implementing a neural network
- Training the neural network to learn how to solve a muddled cube
- Testing the neural network against an unseen muddled cube
Cube AI performed well in testing with restricted difficulty levels. Tests indicate that more difficult cubes can be solved with more training.
Cube AI is implemented in Typescript using node.js.
Modelling
A cube is modelled as an object with Faces. The cube has 6 faces and can perform 6 actions.
- Rotate X axis column 1
- Rotate X axis column 3
- Rotate Y axis column 1
- Rotate Y axis column 3
- Rotate Z axis column 1
- Rotate Z axis column 3
Through these simplified actions all moves can be achieved.
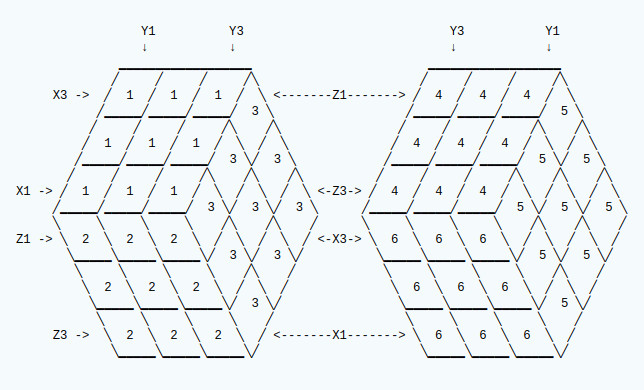
Cube Axis
Rotate actions apply to each face as follows:
Neural Network
This solution uses a single layer neural network to map input tuples to a set of output nodes via weights. There is one output node for each possible action.
Single Output Node
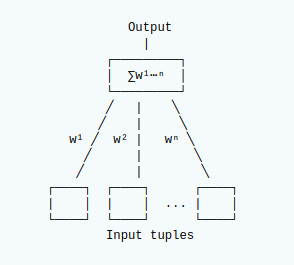
Each distinct tuple has a mapping to each output node. The mapping has a weight associated with it (w¹…wⁿ). When a set of tuples is presented to each node, the sum of the weights for each node is calculated. The node with the greatest output triggers the associated action.
Training
When training the network, data is presented as a set of tuples. Where a tuple is a collection of values representing a selection of the input source.
The tuples are matched to a weight for each node. If the tuple has not been seen before then a new weight is created for it with an initial value of 1 associated with each node. The network calculates the output for each node to determine which node should be triggered and then adjust the weighting for each tuple on the triggered node based on whether the outcome was correct or not. If the outcome was correct then the weighting is increased to re-enforce the selection, otherwise the weighting is decreased to discourage the selection.
Weight adjustments are applied using the following formula.
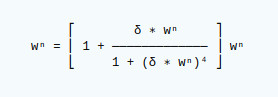
Where `wⁿ` is the weight for node n, `δ` is +1 for a correct outcome and `δ` is -1 for an incorrect outcome. This formula ensures that weight adjustments are applied gradually.
Solving the Cube
Learning Moves
In order to solve the cube the system needs to learn to recognise what moves are appropriate for the state of a muddled cube. This is achieved by muddling a new cube and training the neural network to select the appropriate action to reverse the move made at each stage. The system will then attempt to solve the muddled cube to evaluate training progress.
Note: Training moves are in reverse so that the network can be trained to select the forward move to get back to the previous state.
Training is performed based on a difficulty setting that determines how many moves to learn against a new cube. This process is repeated for n number of training cycles, each time using a different random seed to ensure that the moves are varied and that solution moves are re-enforced.
The bigger the training difficulty the greater the number of possible states, and the more training cycles that are needed.
Cube State
The state of the cube is presented to the neural network as a set of tuples constructed from the moving edges pieces of the cube. All sides of the edge piece are included to represent the piece orientation. The edge pieces are grouped in set of 3 to make a tuple that represents the edge.
There are 12 edges in total representing the edges:
- Axis X3, face 1
- Axis X1, face 1
- Axis Y1, face 1
- Axis Y3, face 1
- Axis X3, face 6
- Axis X1, face 6
- Axis Y3, face 6
- Axis Y1, face 6
- Axis Y1, face 2
- Axis Y3, face 2
- Axis Y3, face 4
- Axis Y1, face 4
Each tuple has a numeric representation of its position on the cube. The face colours are ordered by their face number for ease of visualisation.
Example tuple for the edge pieces on the X1 axis for face 1:
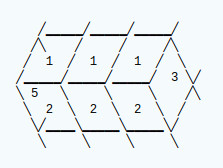
This is represented as the tuple set:
[111, # Numeric representation of axis X1 face 1 1, 2, 5, # Colour values of the 1st piece 1, 2, # Colour values of the 2nd piece 1, 2, 3] # Colour values of the 3rd piece
Testing
The system is presented with an unseen muddled cube and attempts to solve the puzzle. This process requires presenting the cube state to the neural net and applying the triggered action. This process is repeated until the cube is complete or a maximum number of moves have been applied.
Results
When training with 1 million cycles, and a difficulty of 5 moves, the system is able to complete the training cubes 77% of the time. When the trained system is applied to unseen cubes the system is typically able to solve 75%.
Increasing the difficulty to 6 reduces the completion rate during training to 65% and similarly unseen cube completion drops to around 66%. A training difficulty of 7 yields a completion rate of 50%. This indicates that the greater the training difficulty the more training is required.
When training with 3 million cycles, and a difficulty of 7 moves, the system is able to complete the training cubes 52% of the time, but typically able to solve 71% unseen cubes.