M-AI-ZE

This is an experimental AI project. The initial objective is to create a neural network that can solve a maze.
To achieve this goal the I had to overcome the following challenges:
- Generating a random maze
- Implementing a neural network
- Modelling the runner view in the neural network
- Generating a 3D view
M-ai-ze performs well. Tests show that the more the maze is explored early on the better be the AI is at solving it with a direct route.
M-ai-ze is implemented in Typescript with a React UI, backed by Redux toolkit and 99% test coverage.
M-ai-ze is available at m-ai-ze.cmatts.co.uk.
Modelling
The maze is represented by a Maze object that has a specified number of rows and columns forming a grid. An algorithm is used to generate the maze within the allotted grid and sets down a path using row and column references. The algorithm also sets where the exit is located. Internally this is represented as an array of strings with accessor methods to identify whether coordinates are a path or an exit. All coordinates outside the maze bounds are considered walled off. This experiment uses Eller’s algorithm to generate the maze.
The runner is has a direction, and a grid location reference. The runner can change direction, and advance in that direction if it is not walled off. The runner starts in the farthest cell from the exit.
Presentation
The Maze is presented in a 2D overhead view and in a 3d runner view. The speed of the runner can be controlled via a control panel.
The 2D view shows the maze with the runner. The exit is marked with a flag, and the runner is shown with an arrow indicating the direction of travel.
The 3D view shows the runner view as the runner moves through the maze. The exit is indicated with a flag as the runner approaches. This view also shows the number of moves taken and the attempt number. When the runner finds the exit, the run history is displayed.
The control panel enables the user to start and stop the runner, change the speed of the runner and reset the maze.
Maze Generation
A maze is generated using Eller’s Algorithm to create a random maze. For test purposes the randomizer can be seeded to ensure repeatable test cases.
Eller’s Algorithm
Eller’s algorithm is a simple algorithm that quickly generates a maze where every cell in the grid is reachable. It works by creating a row at a time. Each row is generated following the steps below:
- Initialise all cells (columns) for the row that have not been initialised. A new cell will have a wall to the west and a wall to the south and be assigned to a unique group or set. Note: some cells for a row may have already been intialised whilst creating a previous row.
- For all but the last row, break down the west wall for randomly selected cells in the row where the cell to the left belongs to a different group and migrate the group cells to the same group. Migrating the joined cells to the same group ensures that there are no loops in the maze. Note: The first cell in a row must keep its left wall to prevent holes in the maze.
- For the last row, break down the west wall for all cells in the row where the cell to the left belongs to a different group. This is done to ensure that all remaining groups are connected and all cells are reachable.
- For all but the last row, break down at least one cell south wall for every unique group in the row . When breaking through the south wall, initialise the cell below it in the next row assigning it to the same group.
The exit is set at the first cell in the maze and the cells are used to generate the Maze object representation.
Neural Network
This solution uses a single layer neural network to map input tuples to a set of output nodes via weights. There is one output node for each possible action.
Single Output Node
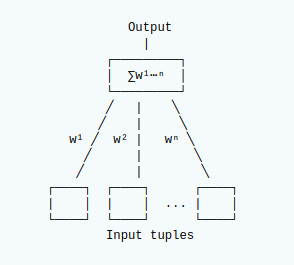
Each distinct tuple has a mapping to each output node. The mapping has a weight associated with it (w¹…wⁿ). When a set of tuples is presented to each node, the sum of the weights for each node is calculated. The node with the greatest output triggers the associated action.
Training
When training the network, data is presented as a set of tuples. Where a tuple is a collection of values representing a selection of the input source.
The tuples are matched to a weight for each node. If the tuple has not been seen before then a new weight is created for it with an initial value of 1 associated with each node.
The network calculates the output for each node to determine which node should be triggered and then adjust the weighting for each tuple on the triggered node based on whether the outcome was correct or not.
If the outcome was correct then the weighting is increased to re-enforce the selection, otherwise the weighting is
decreased to discourage the selection.
Weight adjustments are applied using the following formula.
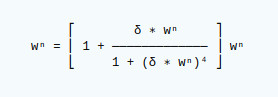
Where `wⁿ` is the weight for node n, `δ` is +1 for a correct outcome and `δ` is -1 for an incorrect outcome.
This formula ensures that weight adjustments are applied gradually.
Solving the Maze
Learning the Route
In order to learn the route the runner must learn to recognise the path it has taken and avoid retracing its steps. The neural network is used to determine the direction of travel based on what the runner can see in each direction. For this experiment the neural net is configured for continual learning. There’s no positive re-enforcement as we don’t know whether a path is correct, only negative re-enforcement is applied to travelling in the opposite direction each time a step is taken. Similarly, when the move is into a wall, the move is blocked, and the neural net is discouraged from making that selection again. Using this simple learning mechanism, when the runner reaches a dead end the neural net will start retracing the steps and find another route that has not been traversed.
Runner View
The runners view of the maze is based on what is visible up to a limited number of steps ahead in each direction. i.e. The view ahead in any direction is limited by any wall immediately ahead, and the runner is able to see openings in the walls along that route. The number of steps visible is 10.
The view is given a binary representation for the left wall, center path, and right wall, where 1 represents a wall and 0 represents a path way. The least significant bit it the closest point, and the most significant bit is always set to 1 to indicate the depth of what can be seen. These views are converted to numeric values and make the tuples presented to the neural net as the view in each direction. An additional attribute for view direction is added to the tuples to enable the neural net to get directional context which will help with the movement decisions.
Example tuples presented for the runners view:
...
### ### ### ### # ###
# # # # # # #
# ### # ##### ### # #
# # # # # # #
# # # ####### #######
# ▶ #
#####################This is represented as the tuple set:
[
[ // North view
0b111110
0b100000,
0b101110,
1
],
[ // East view
0b1111111111,
0b1000000000,
0b1011111110,
2
],
[ // South view
0b10,
0b10,
0b10,
3
],
[ // West view
0b101010,
0b100000,
0b111111,
4
],
]Testing
The runner is presented with a new randomly generated 21×21 grid (10×10 cells) maze to solve. The runner will run the maze until it finds the exit. On the next run the runners position is reset to the start. This can be repeated as many times as desired.
Results
The results of this experiment are very good. The first run is an exploratory run. The more of the maze that is explored, the better the runner performs on subsequent runs.
On a difficult maze where the runner took 2415 moves to find the exit on the first run, the subsequent runs were able to find the exit more directly, completing in 52 and 45 moves. As the runner is continually learning, it will continue to refine the correct path with each attempt until it has the most direct route.
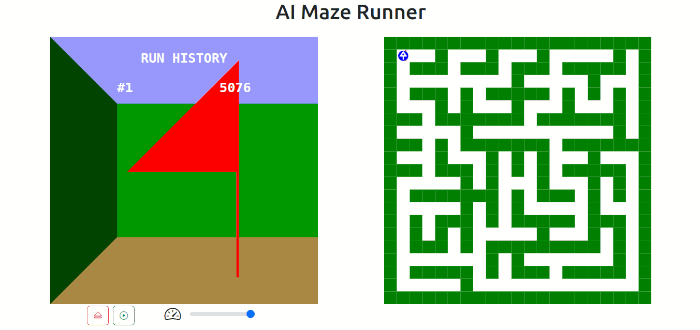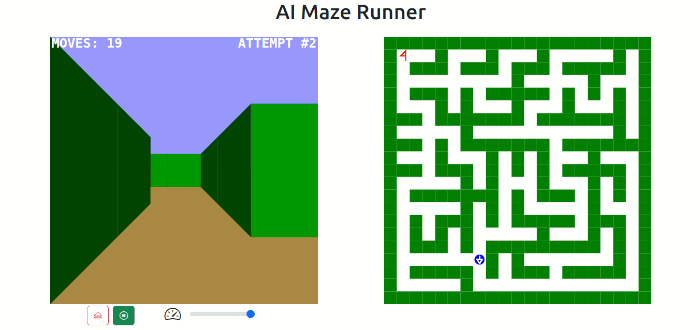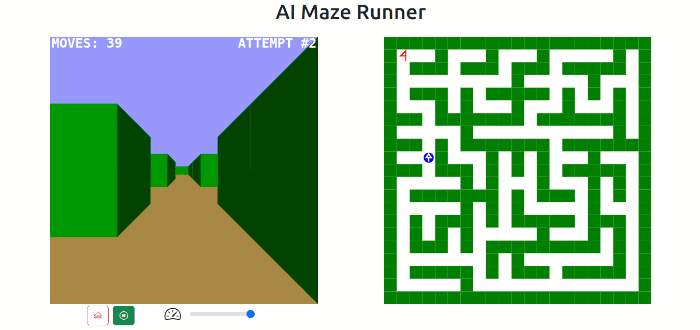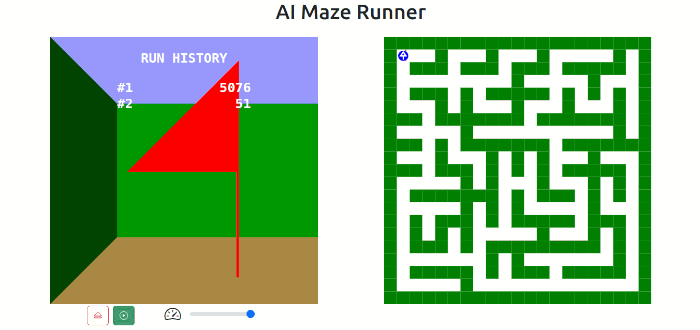
The continual learning may also result the runner getting a bit lost along the way on subsequent runs. This can be the case when the runner solves the maze very quickly having explored very little. On a simple maze where the runner found the exit in 158 moves, the runner took a detour on the second run that led to it finding the exit in 2380 moves. However, on subsequent runs it refined the route to a more direct route completing in 61 moves.
In conclusion, the runner is typically able to find a fairly direct route out of the maze with few misplaced steps by the 2nd attempt and continues to improve on this until it has the perfect path.